维吉尼亚密码的破解
一、引言
上一章我们介绍了维吉尼亚密码的原理,是通过移位替换的加密方法进行加密,但是因为概率论的出现这种简单的移位或替换就容易破解了,其原理很简单,英文中字母出现的频率是不一样的。比如字母 e 是出现频率最高的,占12.7%;其次是t,9.1%;然后是a,o,i,n等,最少的是z,只占**0.1%**。
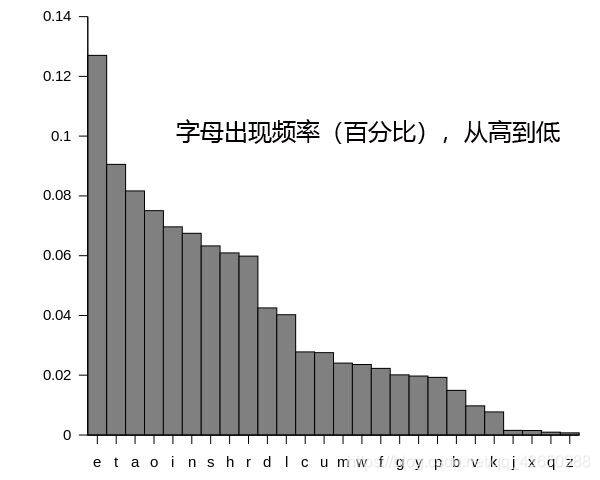
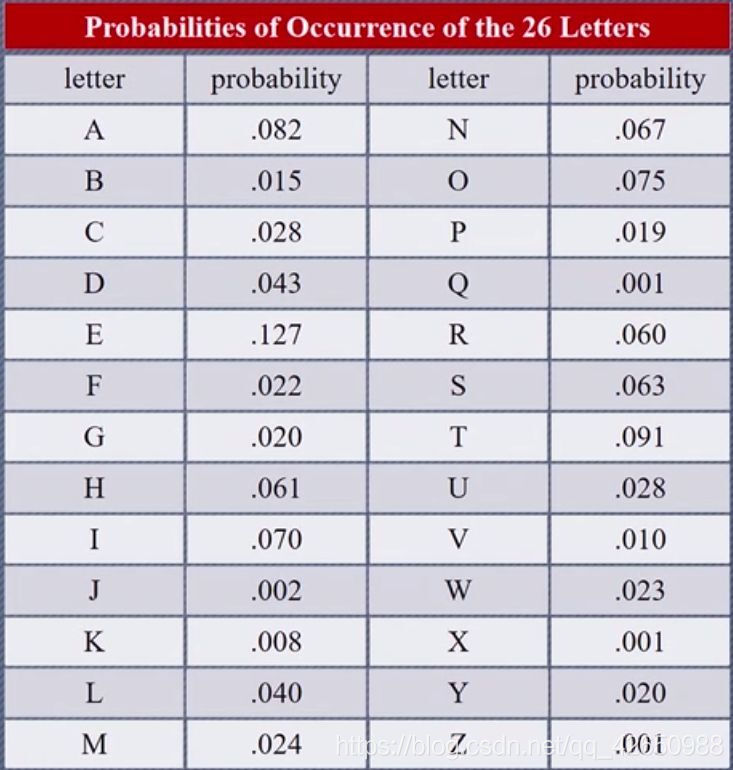
除了英语,其他语言也有相关统计(图片来源)
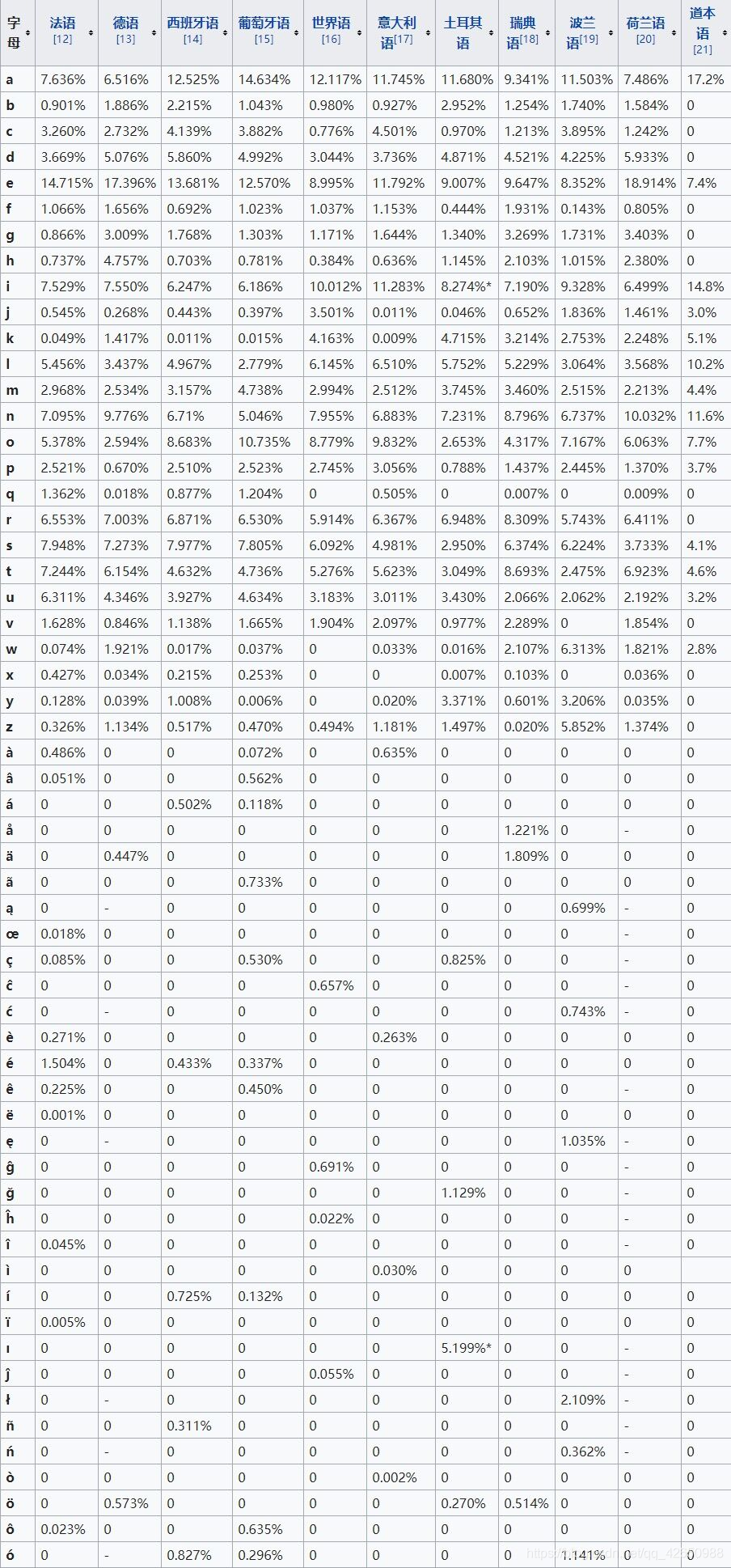
二、一般破解的方法
1. 穷举密钥搜索
只适用于与小的密钥空间,而像维吉尼亚密码的 $Z^n_{26}$ 是 26 的 n 次方的空间,当 n 很大时,计算量是相当大的。
2. 频率统计
单表代换
移位密码: 相同的明文字母总是对应相同的密文字母,因此,尽管字母的外形改变了,他出现的概率还是不变的,只要根据足够多的样例来进行统计,最终密文字母的出现概率总是近似于明文字母的出现概率,并且与之一一对应。
多表代换
维吉尼亚密码: 相同的明文字母可能对应不同的密文字母,这里讲的维吉尼亚密码的破解也是根据字母出现的频率的蛛丝马迹进行破解。
三、维吉尼亚密码的破解
1. 确定密钥长度
方法一:Kasiski测试法
原理:密文中出现两个相同字母组,它们所对应的明文字母相同的可能性很大,这样的两个密文字母组之间的距离可能为密钥长度的整数倍。
尽管在维吉尼亚密码中相同的明文可能对应不同的密文,但是若连续出现相同的密文,那么用同样的密钥加密的概率会大大增加。这里密文 $ZB$ 都是用 $HI$ 加密,计算两者之间的距离为 $5$,因此可推断出来密钥长度为 $5.$
方法二:重合指数法
原理:自然语言(以英语为例)的重合指数约为 0.065,而且单标代换不会改变该值。
重合指数定义:
设 $$x=x_1x_2…x_n$$ 是含有 $n$ 个字母的串,则在 $x$ 中随机选择两个元素且这两个元素相同的概率为:
定义:$f_i$ 为 26 个字母中第 $i$ 个字母在 $x$ 中出现的次数
[例如:$x=AAZZZ,n=5,f_0=2,f_{25}=3$,第一次取出 A 的概率为 $\frac {f_0} {n}$,第二次再取出 A 的概率为 $\frac {f_0} {n} * \frac {f_0-1} {n-1}$]
当我们把 26 个字母的概率全部相加,得到的总的概率就是重合指数:
$$
I_c(x)={\frac {\displaystyle\sum_{i=0}^{25}f_i(f_i-1)} {n(n-1)} }
$$
当计算的数量很大时,我们将 $n(n-1)$ 近似为 $n^2$,将 $f_i(f_i-1)$ 近似为 $f_i^2$
因此
$$
I_c(x) \approx \displaystyle\sum_{i=0}^{25} {p_i^2} \approx0.065
$$
这里的 $p_i$ 表示第 $i$ 个字母在英语语言中出现的概率,就是在引言中列出的数值。
这个数值非常重要。
注意:在单表代换中,不会改变该值,也就是用相同密钥字加密应服从相同的重合指数。
猜测密钥长度
假设密钥长度为 $d$,提取相同密钥字加密的密文,测试其重合指数。
如果猜测正确,则重合指数接近 $0.065$,否则字符串表现得更加随机一般在 $0.038(1/26) \thicksim 0.065$ 之间。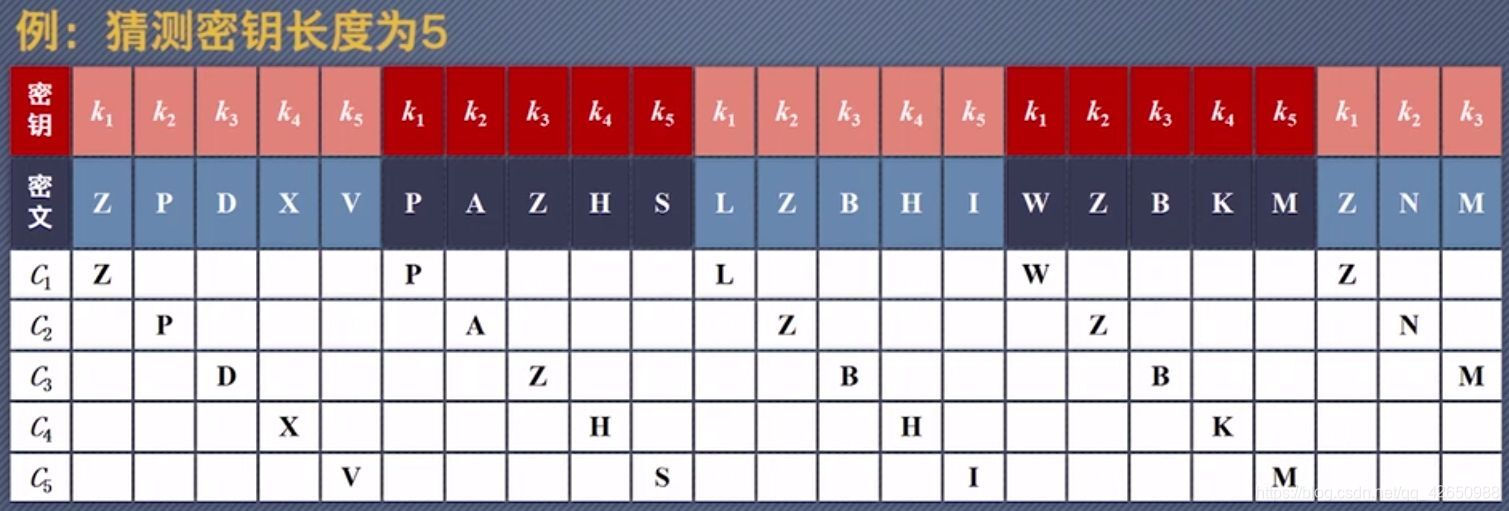
在这里,我们先猜测密钥长度为 5,然后将密文按照 5 进行分组,分别提取出用密钥 $k_1,k_2,k_3,k_4,k_5$ 加密的密文,组成集合 $C_1,C_2,C_3,C_4,C_5$,这样就把多表代换转化成了单表代换。
这里 $C_1={Z,P,L,W,Z},C_2={P,A,Z,Z,N},C_3={D,Z,B,B,M},C_4={X,H,H,K},C_5={V,S,I,M}$
以一个例子为例: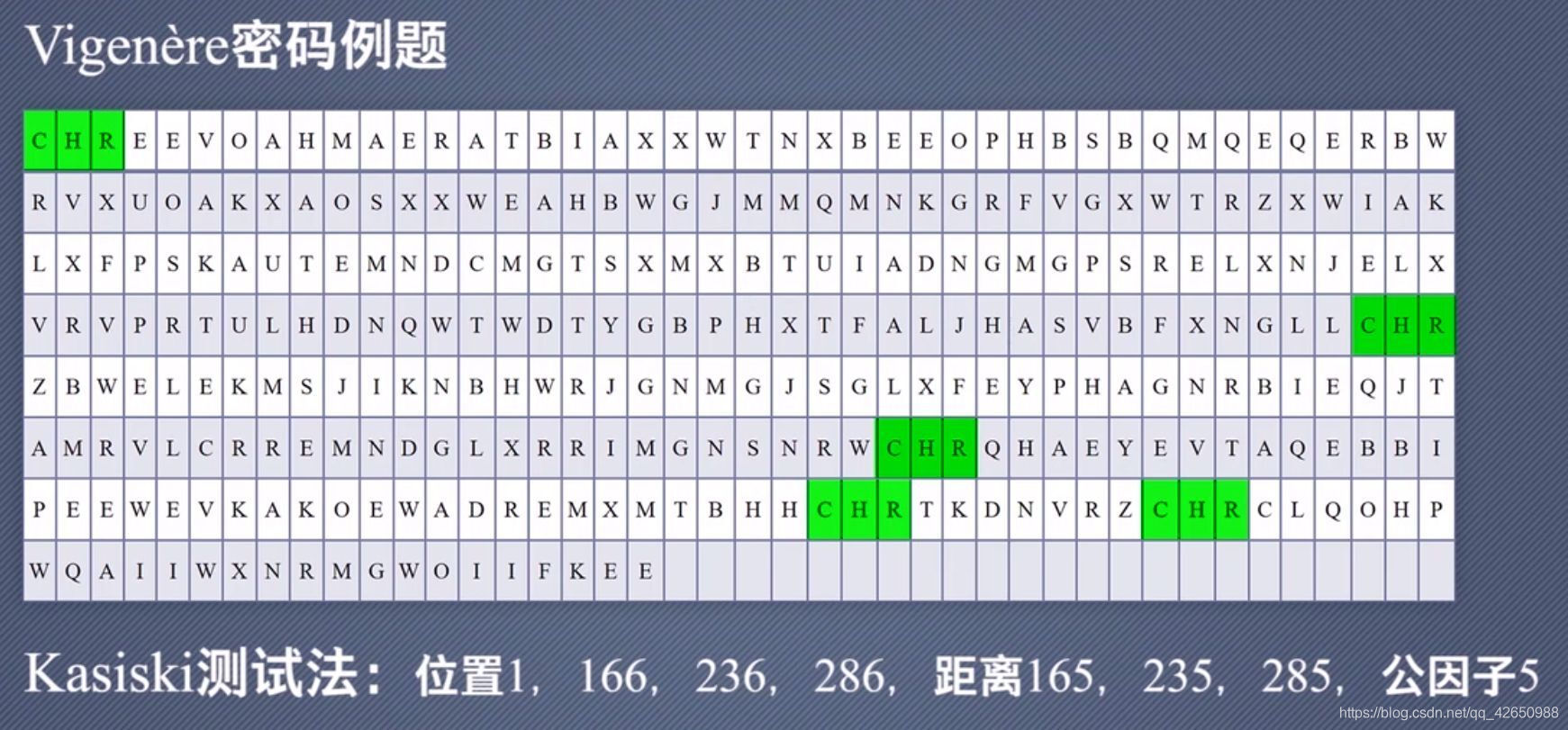
$CHR$ 这三个字符出现频率较高,因此我们将其位置记录下来,测算他们之间的距离,并取最大公因数 5,猜测 5 便是密钥长度。这很有可能是相同的明文被相同的密文加密了。其实很容易猜到,这很可能是英语当中的定冠词 the.
我们在用重合指数法进行测试,分别测试 $d=1,2,3,4,5$ (过程略)
| $d$ | 重合指数 |
|---|---|
| $1$ | $[0.045]$ |
| $2$ | $[0.046,0.041]$ |
| $3$ | $[0.043,0050,0.047]$ |
| $4$ | $[0.042,0.039,0.046,0.040]$ |
| $5$ | $[0.063,0.068,0.069,0.061,0.072]$ |
观察发现,只有当 $d=5$ 的时候,重合指数接近 $0.065$,因此刚刚的猜测 $d=5$ 是正确的,这时通过穷举密钥的复杂度为 $26^5$,但是仍然比较大。
2. 确定密钥字相对位移
密钥字的相对位移实际上就是确定密钥之间的相互关系。
这里引入一个定义:
重合互指数:
设 $x=x_1,x_2,…,x_n,y=y_1,y_2,…,y_{n’}$,分别为长度为 $n$ 和 $n’$ 的串,其重合互指数为从 $x$ 和 $y$ 中分别随机选出一个元素且两个元素相同的概率。
计算方法和刚刚的计算方法类似:
$$
MI_c(x,y)=\frac{\displaystyle\sum_{i=0}^{25}f_if’_i}{nn’}
$$
具体不再阐述。
考虑不同密钥字加密后密文串的重合互指数,设密钥字为 $k=k_1k_2…k_d$,$C_i$ 中的一个字母与 $C_j$ 中的一个字母都是 $A$ 的概率为 $p_{0-k_i}p_{0-k_j}$.
其中 $p_{0-k_i}$ 为密文 $A$ 所对应明文字母的出现概率。同理可以计算 $B,C,D,…,Z$,因此:
$$
MI_c(C_i,C_j) \approx \displaystyle\sum_{l=0}^{25}p_{l-k_i}p_{l-k_j}=
\displaystyle\sum_{l=0}^{25}p_lp_{l+k_i-k_j}=\displaystyle\sum_{l=0}^{25}p_{l-k_i+k_j}p_l
$$
这里的下标是需要对 26 取模的,可以观察到:$Mi_c$ 取决于相对位移 $k_i-k_j$.
移位表如下: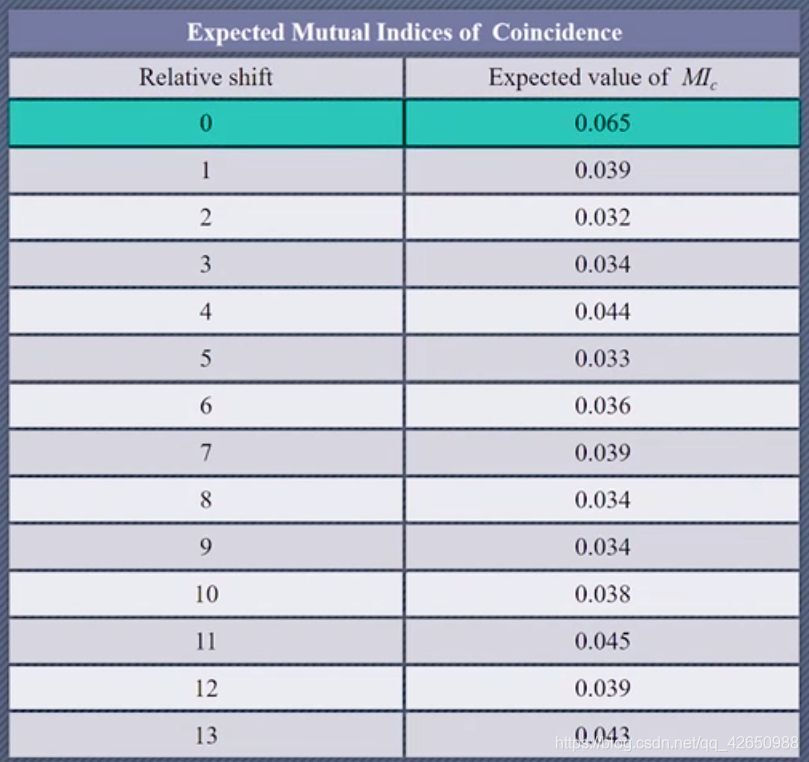
观察这里当相对距离为0时,重合互指数为 $0.065$,在之前提到的自然语言的重合互指数也是 $0.065$,这并不是巧合。当相对位移位 0 时,其实就是 $C_1,C_2$ 的集合是用同一种密文加密得到,这也就是单表代换这样,并不会改变重合指数。
这里其实并不需要列举从 0 到 25 的所有值。
猜测不同密钥字的相对位移s(猜测范围0~25)
$$
MI_c(C_i,C_j)=\frac{\displaystyle\sum_{t=0}^{25}f_{i,t}f_{j,t-s} } {n_in_j}
$$
这里 $n_i$ 是指集合 $C_i$ 中字符个数,这里 $n_j$ 是指集合 $C_j$ 中字符个数,$f_{i,t}$ 表示在集合 $C_i$ 中,$t$ 这个密文字符出现的次数,$f_{j,t-s}$ 表示在集合 $C_j$ 中,$t-s$ 这个密文字符出现的次数。
如果猜对 $s$,那么 $MI_c$ 应该接近 $0.065$,这意味着找到了不同密钥字加密的相同的明文字母,这也就找到了密钥字之间的相对位移,也就转化成了单表代换。
这里用 $m$ 表示明文字母,$c,c’$ 分别表示 $C_i,C_j$ 中 $m$ 对应的密文字母,那么:
$$
m=c-k_i \pmod{26} \ m=c’-k_j \pmod{26}
$$
实际上,在维吉尼亚密码中,并没有很好的隐藏密钥和密文之间的相互关系,密钥之间的相互差距会体现在密文之间的相互关系。
我们计算上面例子中的集合 $C_1,C_2,C_3,C_4,C_5$ 两两之间的重合互指数:
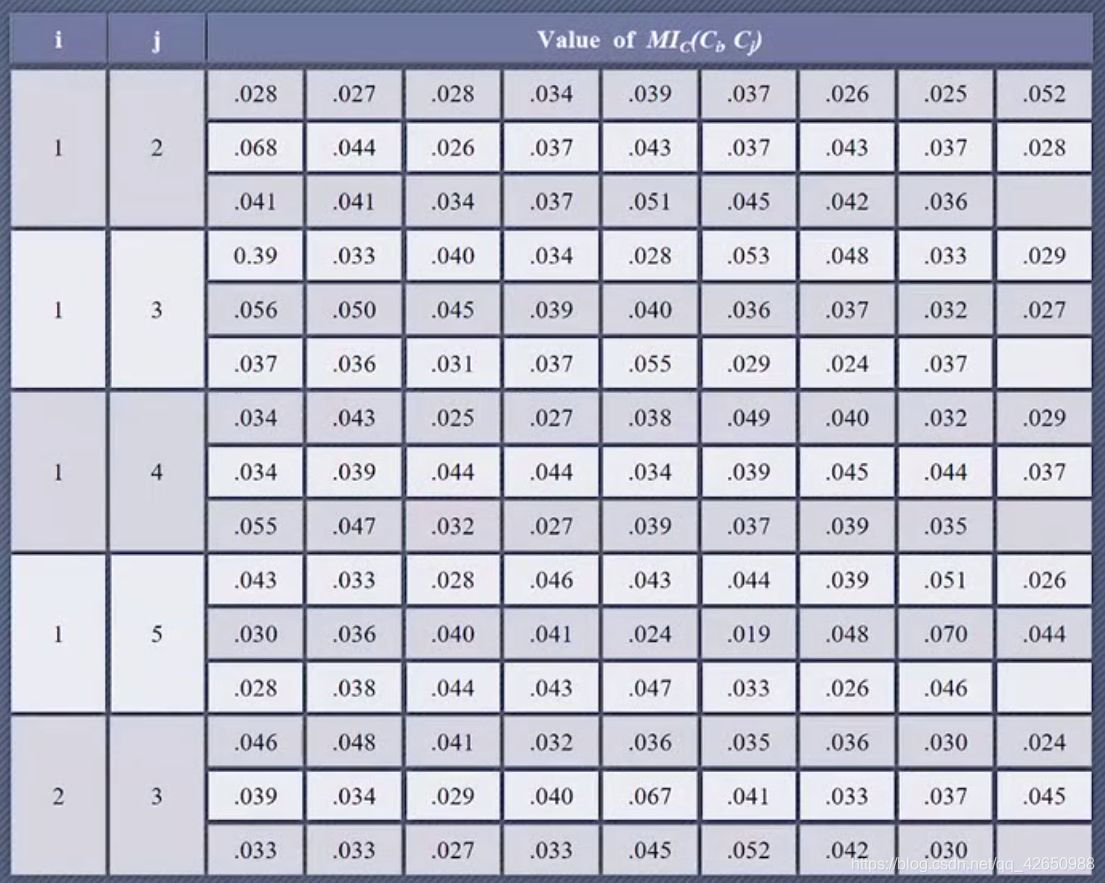
这里的 $i,j$ 表示当取到不同集合的时候,后面的值表示当猜测的相对位移 $s$ 取不同值的时候重合互指数的结果。
我们观察结果,当 $i=1,j=2,s=9$ 时,重合互指数达到了 $0.068$,因此可以得到 $k_1-k_2=9$.
但是当 $i=1,j=3;i=1,j=4$ 时,没有合适的相对位移,那么我们先暂时跳过,观察其他结果,发现当 $i=1,j=5,s=16$ 时,重合互指数达到 $0.070$,$i=2,j=3,s=13$ 的时候,重合互指数达到了 $0.067$.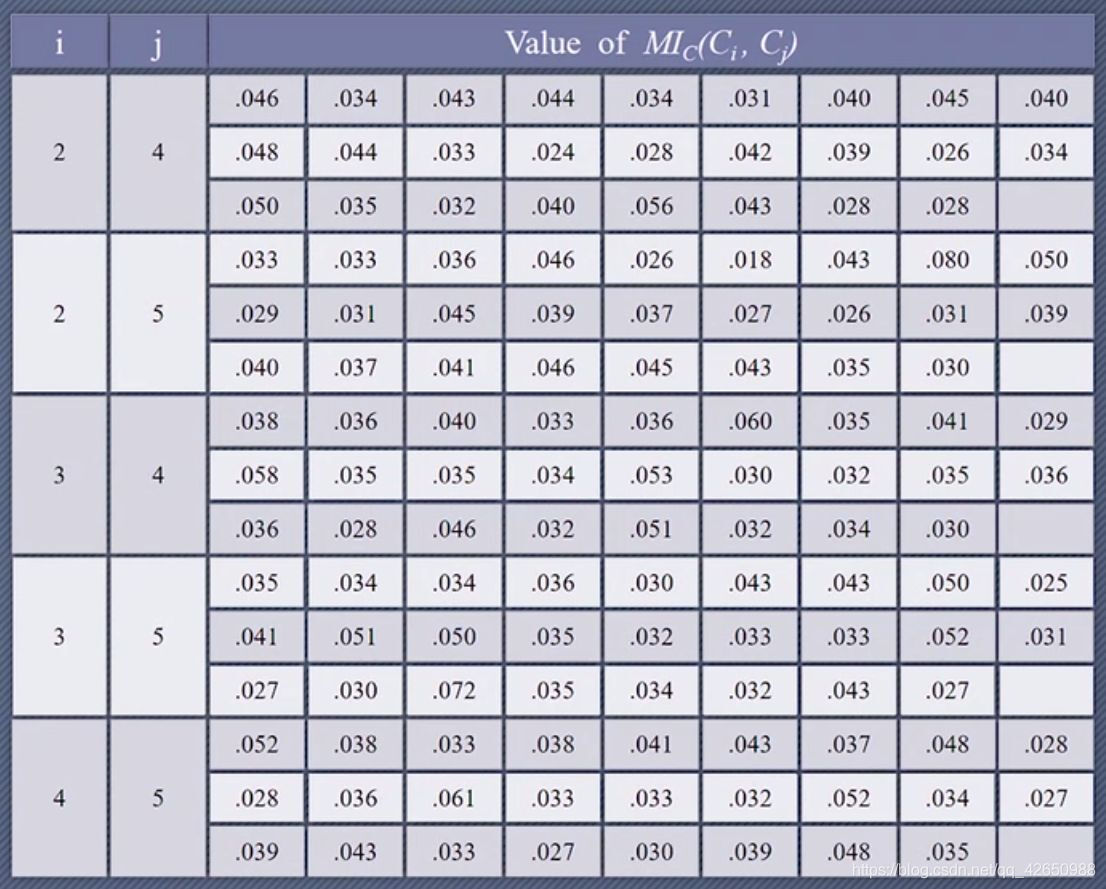
我们列举完剩下的结果,得到:
$$
k_1-k_2=9 \ k_1-k_5=16 \ k_2-k_3=13 \ k_2-k_5=7 \ k_3-k_5=20 \ k_4-k_5=11
$$
3. 穷举搜索密钥字
根据上述的结果,在确定密钥字之间关系式的基础上,只要穷举 $26$ 中可能性就可以了。因为当猜测 $k_1$ 的时候, $k_2$ 也就确定下来了,以此类推,剩下的几个密钥也就确定下来了,只要从 $A-Z$ 进行穷举即可。
四、总结
一个好的密码加密方案(或者说是算法),应该要很好的隐藏密钥和密文之间的联系,通过更复杂的算法或者在更大的密钥空间中,可以有效避免穷举搜索破解。如何设计加密算法以及如何选择合适的密钥空间,将在今后继续学习。